Geometric Progression Sum to Infinity
A n ar n-1. The sum of the infinite GP formula is given as S n a1r where r.

Geometric Series Sum To Infinity Examsolutions Youtube
Where b 1 - is the first element of the geometric series in our case it.
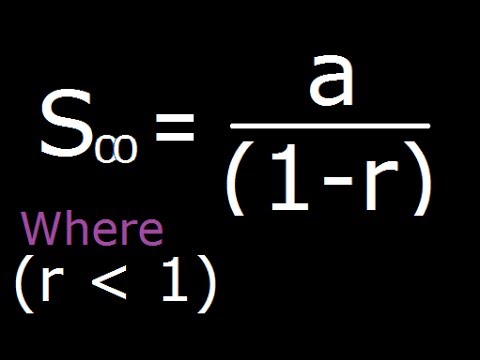
. N will tend to Infinity n Putting this in the generalized formula. Since 1 1 2 a and 1 2 r then 1 2 1. Doc 6 pages.
Geometric series Jhon Paul Lagumbay. Therefore to calculate series sum one needs somehow to find the expression of the partial series sum S nIn our case the series is the decreasing geometric progression with ratio 13. By Remberto Coaquira Choque.
Quantitative Aptitude Doc 6 pages. 36 You have already learned how to find the sum. The NCERT Solutions for Class 10 Maths Chapter 5 PDF file available for free can help students to score good marks.
You can add n Terms in GP Geometric Progression very quickly through this website I have to calculate the value of pi from the infinite series. How to prepare for Quantitative Aptitude for CAT with EduRev Doc 8 pages. In geometric progressions where r 1 in other words where r is less than 1 and greater than 1 the sum of the sequence as n tends to infinity approaches a value.
Where r is a constant which is known as common ratio and none of the terms in the sequence is zero. 120 days study plan to prepare for CAT with EduRev Doc 4 pages. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms.
1 2 4 8 16 32 64 128 256. This is basic math used to perform the arithmetic operation of addition of. The Product of all the numbers present in the geometric progression gives us the overall product.
Each successive term is obtained in a geometric progression by multiplying the common ratio to its preceding term. S n b 1 q n 1 q 1. Advice to Aspirants - CAT.
In Maths NCERT Solutions Class 10 Chapter 5 students will learn about the arithmetic progression. What all will you get under EduRev Infinity Package for CAT. Averages - Quantitative Aptitude Quant 7 videos 5 docs 5 tests.
This sequence has a factor of 2 between each number. For example the series is geometric because each successive term can be obtained by multiplying the previous term by In general a geometric series is written as where is the coefficient of each term and is the. 2 4 8 16 Solution.
It is known that the sum of the first n elements of geometric progression can be calculated by the formula. A Policy on Geometric Design of Highways and Streets. 12 a The first term of an arithmetic progression is 5 and the fifth term is 7.
In the following series the numerators are in. The squared terms could be 2 terms 3 terms or n number of terms first n even terms or odd terms set of natural numbers or consecutive numbers etc. 4 b A geometric progression has third term of 8 and sixth term of 0064.
It is not the case for all types of sequences though. For example 2 4 6 8 10 is an AP because difference between any two consecutive terms in. A Sequence is a set of things usually numbers that are in order.
Sum of squares refers to the sum of the squares of numbers. In other words if you keep adding together the terms of the sequence forever you will get a finite value. Find the sum to infinity of this progression.
This file is prepared by the best academic experts in India. Product of the Geometric series. The formula works for any real numbers a and r except.
A POLICY on GEOMETRIC DESIGN of HIGHWAYS and STREETS 2001 American Association of State Highway and Transportation Officials. Download Free PDF Download PDF Download Free PDF View PDF. An arithmetic-geometric progression AGP is a progression in which each term can be represented as the product of the terms of an arithmetic progressions AP and a geometric progressions GP.
A geometric series is the sum of the numbers in a geometric progression. Vietas formula can find the sum of the roots 3 5 2 big 3-5 -2big 3 5 2 and the product of the roots 3 5 15 big3 cdot -5-15big 3 5 1 5 without finding each root directly. 1 1 2 S Example 2.
. Geometric Sequences and Sums Sequence. While this is fairly trivial in this specific example Vietas formula is extremely useful in more complicated algebraic polynomials with.
The sum to infinity of a geometric progression. Download Free PDF Download PDF Download Free PDF. It is basically the addition of squared numbers.
In a Geometric Sequence each term is found by multiplying the previous term by a constant. In the example above this gives. In simple terms it means that the next number in the series is calculated by adding a fixed number to the previous number in the series.
Letting a be the first term here 2 n be the number of terms here 4 and r be the constant that each term is multiplied by to get the next term here 5 the sum is given by. The arithmetic and geometric progression Maija Liepa. Sum Of Geometric Series Calculator.
Snape apologizes to harry fanfiction. For Infinite Geometric Series. The formula for the nth term of a geometric progression whose first term is a and common ratio is r is a n ar n1.
Now learn how t o add GP if there are n number of terms present in it. Arithmetic Progression Sum of Nth terms of GP. Every answer is written according to the.
A geometric series is a sum of an infinite number of terms such that the ratio between successive terms is constant. A sequence of numbers is called an Arithmetic progression if the difference between any two consecutive terms is always the same. If you pick another one for example a geometric sequence the sum to infinity might turn out to be a finite term.
What is the sum to infinity of 1 1 3 1. Students can download this PDF file by visiting Vedantu. This value is equal to.
Find the sum of the first 40 terms of this progression. Since 1 3a and 1 3 r then 3 9. It is very useful while calculating the Geometric mean of the entire.
Each term except the first term is found by. Intuitively the sum of an infinite number of terms will be equal to infinity whether the common difference is positive negative or even equal to zero. 1 4 1 3 S 41.
Pi4 - 43 45 47 49 -411 As a test if you input resistances of 3 9 and 18 ohms your answer should be 2 ohms As a test if you input. What is the sum to infinity of 1 1 1 1. N th term for the GP.

Proof Of The Geometric Series Formula Finite Infinite Youtube
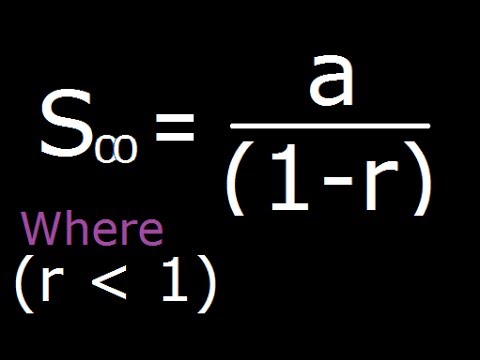
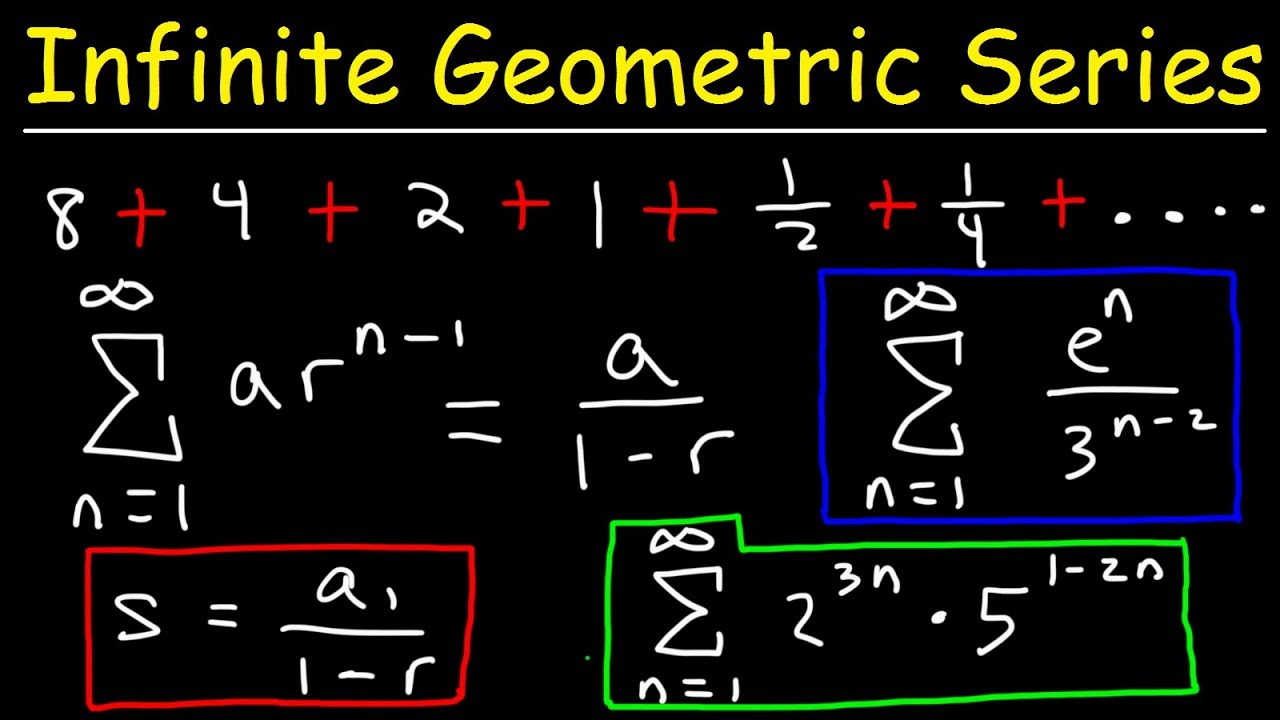
Geometrical Progression Sum Of Infinite Terms Derivation Youtube

No comments for "Geometric Progression Sum to Infinity"
Post a Comment